Leggett mode in superconductors and Lifshitz invariant
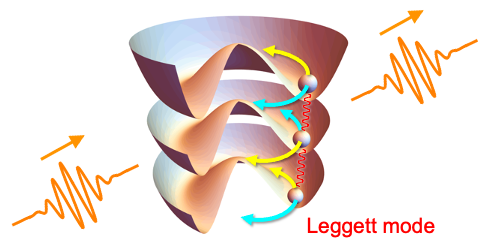
Previously, it has been thought that superconducting orders respond to light only in a nonlinear way [1], except for special situations. However, it has recently been found that certain multiband superconductors can respond to light linearly [2]. More generally, superconducting orders can respond to light linearly if there exists a so-called Lifshitz invariant in the free energy. Whether or not the Lifshitz invariant appears can be classified by the group theory [3]. In particular, the linear optical response is mediated by the Leggett mode, where the different phases of superconducting order parameters oscillate in alternate directions.
[1] Y. Murotani, N. Tsuji, H. Aoki, “Theory of light-induced resonances with collective Higgs and Leggett modes in multiband superconductors”, Phys. Rev. B 95, 104503 (2017).
[2] T. Kamatani, S. Kitamura, N. Tsuji, R. Shimano, T. Morimoto, “Optical response of the Leggett mode in multiband superconductors in the linear response regime”, Phys. Rev. B 105, 094520 (2022).
[3] R. Nagashima, S. Tian, R. Haenel, N. Tsuji, D. Manske, “Classification of Lifshitz invariant in multiband superconductors: An application to Leggett modes in the linear response regime in Kagome lattice models”, Phys. Rev. Research 6, 013120 (2024). [Press release, Youtube.]
Higgs mode in superconductors
In superconductors, there exists a collective mode of an amplitude oscillation of the superconducting order parameter, which is recently called Higgs mode due to the analogy with the Higgs particle in high energy physics (for a review, see e.g., [1][2]). Since the Higgs mode is electrically and magnetically neutral, it has been difficult to couple it with external probes such as light. However, we have found that if one uses an intense terahertz laser one can couple the Higgs mode in superconductors with electromagnetic fields nonlinearly [3]. This coupling has been observed in recent terahertz laser experiments on NbN superconductors [4][5].
[1] N. Tsuji, I. Danshita, S. Tsuchiya, “Higgs and Nambu–Goldstone modes in condensed matter physics”, Encyclopedia of Condensed Matter Physics (2nd ed.), Vol. 1, 174 (2024).
[2] R. Shimano, N. Tsuji, “Higgs mode in superconductors”, Annu. Rev. Condens. Matter Phys. 11, 103 (2020).
[3] N. Tsuji, H. Aoki, “Theory of Anderson pseudospin resonance with Higgs mode in superconductors”, Phys. Rev. B 92, 064508 (2015).
[4] R. Matsunaga, N. Tsuji et al., “Light-induced collective pseudospin precession resonating with Higgs mode in a superconductor”, Science 345, 1145 (2014).
[5] R. Matsunaga, N. Tsuji et al., “Polarization-resolved terahertz third-harmonic generation in a single-crystal superconductor NbN: Dominance of the Higgs mode beyond the BCS approximation”, Phys. Rev. B 96, 020505(R) (2017).
Out-of-time-order fluctuation-dissipation theorem
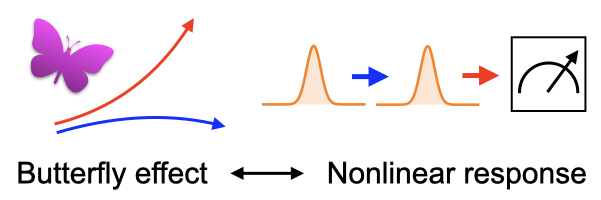
An out-of-time-ordered correlator (OTOC) refers to a correlation function such as <A(t)B(t’)A(t)B(t’)> that does not obey the usual time ordering. OTOCs are expected to be related to chaotic properties of quantum many-body systems and information scrambling. We have found a general relationship among OTOCs, which can be viewed as a higher-order extension of the fluctuation-dissipation theorem (FDT) [1]. While the conventional FDT relates fluctuations in equilibrium and linear response coefficients, the out-of-time-order FDT relates scrambling and certain nonlinear response functions. It also has an application to Maldacena-Shenker-Stanford conjecture, which suggests a universal bound on the exponential growth rate of OTOCs [2].
[1] N. Tsuji, T. Shitara, M. Ueda, “Out-of-time-order fluctuation-dissipation theorem”, Phys. Rev. E 97, 012101 (2018).
[2] N. Tsuji, T. Shitara, M. Ueda, “Bound on the exponential growth rate of out-of-time-ordered correlators”, Phys. Rev. E 98, 012216 (2018).
Nonthermal fixed point and nonequilibrium criticality
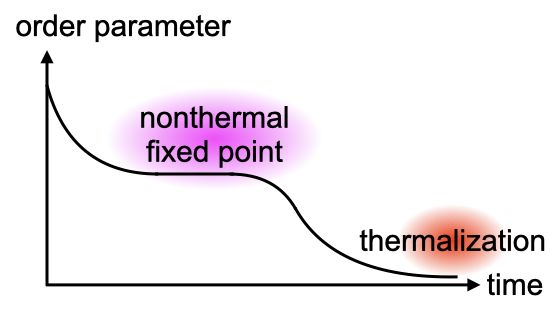
How does a quantum many-body system thermalize in the presence of a long-range order such as antiferromagnetism or superconductivity? In the Hubbard model with a long-range order driven by an interaction quench, the system does not directly relax to thermal equilibrium but stays at a nonthermal fixed point for long time [1][2]. At the fixed point, the long-range order remains to survive even if the effective temperature exceeds the equilibrium critical temperature. By changing the quench strength, there emerges a nonequilibrium critical point, where various physical quantities obey universal scaling laws that are distinct from the equilibrium ones.
[1] N. Tsuji, M. Eckstein, P. Werner, “Nonthermal antiferromagnetic order and nonequilibrium criticality in the Hubbard model”, Phys. Rev. Lett. 110, 136404 (2013).
[2] P. Werner, N. Tsuji, M. Eckstein, “Nonthermal symmetry-broken states in the strongly interacting Hubbard model”, Phys. Rev. B 86, 205101 (2012).
Repulsion-to-attraction transition driven by electric fields
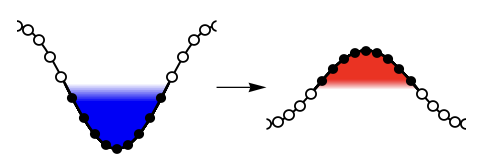
In solids the Coulomb interaction between electrons is always repulsive. However, if one drives electrons on a lattice by ac electric fields with appropriate amplitude and frequency, one can effectively change the interaction from repulsive to attractive [1]. The repulsion-to-attraction transition occurs due to the emergence of Floquet quasiparticles (i.e., photon-dressed states), whose bandwidth is renormalized by the effect of electric fields. When the bandwidth becomes ‘negative’, the driven system approaches a negative-temperature state, where the interaction is effectively switched from repulsive to attractive. Once the strong attractive interaction is realized, superconductivity is expected to emerge at high temperature. One can also induce similar effects by pulsed electric fields [2].
[1] N. Tsuji, T. Oka, P. Werner, H. Aoki, “Dynamical band flipping in fermionic lattice systems: an ac-field driven change of the interaction from repulsive to attractive”, Phys. Rev. Lett. 106, 236401 (2011).
[2] N. Tsuji, T. Oka, H. Aoki, P. Werner, “Repulsion-to-attraction transition in correlated electron systems triggered by a monocycle pulse”, Phys. Rev. B 85, 155124 (2012).
Light-induced Mott insulator-to-Floquet metal transition
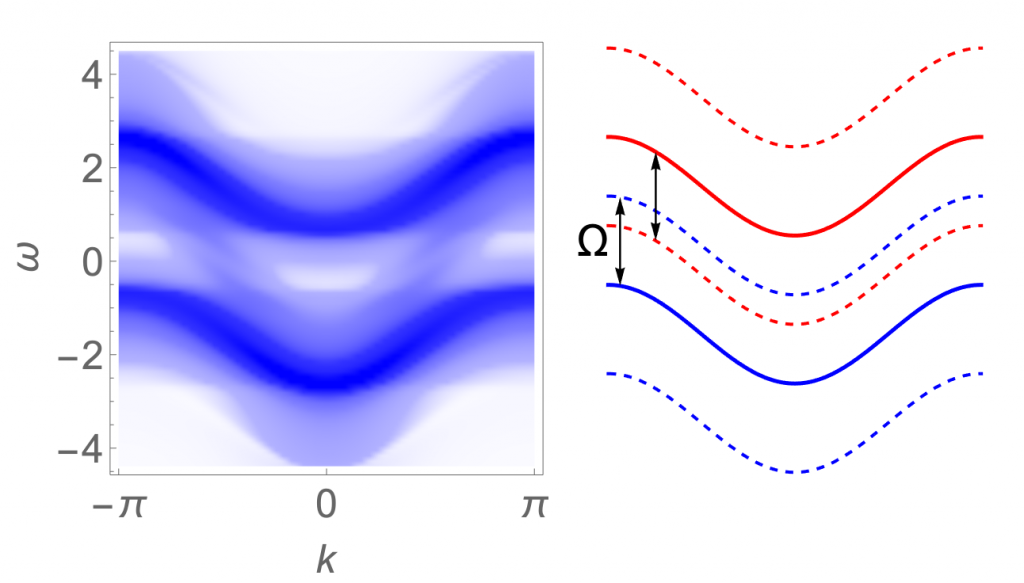
During the laser excitation, the system turns into a so-called Floquet state accompanied by emergent quasiparticles (for a review, see, e.g., [1]). To analyze nonequilibrium time-periodic steady states of correlated electron systems, we have proposed a new method called the Floquet dynamical mean-field theory (DMFT) [2][3]. By applying the Floquet DMFT to the Falicov-Kimball model, we have studied nonequilibrium steady states of a Mott insulator driven by an intense pump light in the presence of dissipation. We have found that a Floquet sideband is created inside the Mott gap, and that such a Floquet metallic state shows anomalous optical responses. In particular, the optical conductivity shows a new resonance structure around the pump frequency, which originates from quantum correction effects unique to nonequilibrium.
[1] N. Tsuji, “Floquet States”. Encyclopedia of Condensed Matter Physics (2nd ed.), Vol. 1, 967 (2024).
[2] N. Tsuji, T. Oka, H. Aoki, “Correlated electron systems periodically driven out of equilibrium: Floquet + DMFT formalism”, Phys. Rev. B 78, 235124 (2008).
[3] N. Tsuji, T. Oka, H. Aoki, “Nonequilibrium Steady State of Photoexcited Correlated Electrons in the Presence of Dissipation”, Phys. Rev. Lett. 103, 047403 (2009).
Nonequilibrium dynamical mean-field theory
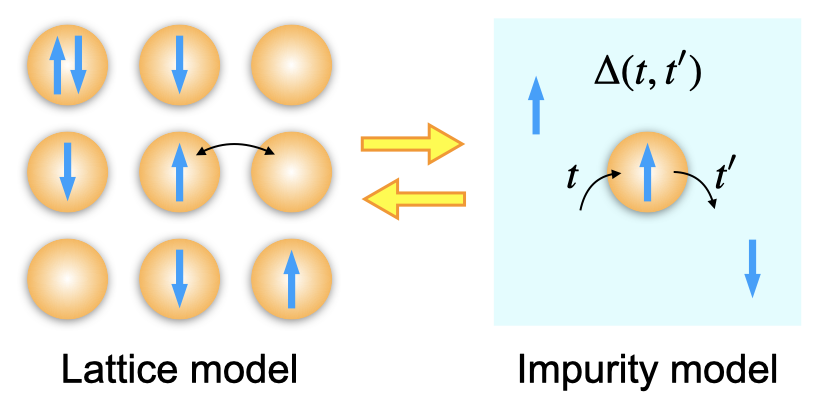
It is in general challenging to theoretically describe nonequilibrium quantum many-bod systems, since one has to take account of non-perturbative effects of interactions and quantum mechanical time evolution at the same time. One of the approaches that have recently been developed for those systems is the nonequilibrium dynamical mean-field theory (DMFT) (see, e.g., a review [1] and a paper [2]). In the nonequilibrium DMFT, a lattice model is mapped to an impurity model embedded in an effective dynamical mean field, which is then solved self-consistently. With this method, it has become possible to study nonequilibrium problems of the Hubbard model (a prototypical model of strongly correlated electron systems) in the thermodynamic limit.
[1] H. Aoki, N. Tsuji, M. Eckstein, M. Kollar, T. Oka, P. Werner, “Nonequilibrium dynamical mean-field theory and its applications”, Rev. Mod. Phys. 86, 779 (2014).
[2] N. Tsuji, P. Werner, “Nonequilibrium dynamical mean-field theory based on weak-coupling perturbation expansions: Application to dynamical symmetry breaking in the Hubbard model”, Phys. Rev. B 88, 165115 (2013).